MAW: Chapter 6 Reflection
Reflection
In chapter 6, we learn about the priority queue ADT. We assume each item has a "priority" and the ADT allows us to insert the element into the queue and get the element with "highest" priority from the queue. The model looks like

and the big picture we have studied so far becomes:
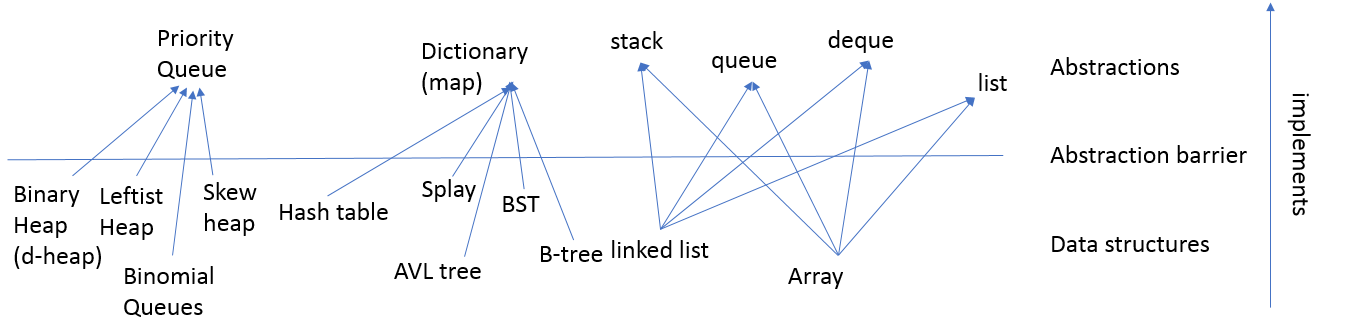
In order to support two operations required by the model, we propose four new implmentations. Binary heap is the most commonly-seen one. Insert can be done in \(O(\log N)\) in the worst case and constant on average. DeleteMin can be done in \(O(\log N)\). However, it has natural drawback in supporting merge operation, which is needed when we want to merge two heaps into one. This leads to the leftist heap. Leftist heap supports all three operations (insert, DeleteMin, merge) efficiently but we needs to maintain extra information in the node and we need to do extra test during merge in order to maintain the leftist heap property. To better solve these two little disadvantages, we propose skew heap, which has no restriction on the tree structure at all while still enjoying the efficiency of operations in amortized time. However, there is still room for improvement because both leftist heap and skew heap cannot support constant on average insertion like binary heap does. This is why we propose a new structure called binomial queue.
There are many applications of priority queues:
- Operating system task scheduler
- Forward network packets in order of urgency
- Select most frequent symbols for data compression
- Sorting
- Implementation for greedy algorithms
Left Out
Some material I left out when I work through this chapter:
- 6.9.c, 6.10, 6.12, 6.20, 6.21, 6.30, 6.32, 6.33, 6.34, 6.35, 6.36