This is the summary of skew heap part in MAW Chapter 6.

Motivation

Like the relation between splay trees and AVL trees, we want to have \(O(\log N)\) amortized cost per operation. In addition, we don't want to have any auxiliary information stored at the nodes. In other words, we want to trade strict \(O(\log N)\) operation for less space we need to use for the data structure. In this case, like splay trees to AVL trees, we have Skew heaps to leftist heaps.

Concept

Skew heaps are binary trees with heap order, but there is no structural constraint on these trees. This means that we don't need the binary tree to be complete (i.e. binary heap) or left heavy (i.e. leftist heap).

In addition, we don't store \(Npl\) information in the node.

Properties

• A perfectly balanced tree forms if the keys \(1\) to \(2^k-1\) are inserted in order into an initially empty skew heap.

Operations

Skew heap is extremely similar with leftist heap in terms of merge operation. There is only one difference: for leftist heap, we check to see whether the left and right children satisfy the leftist heap order property and swap them if they do not. However, for skew heaps, the swap is unconditional. In other words, we always swap the left & right subtrees at each step of merge.

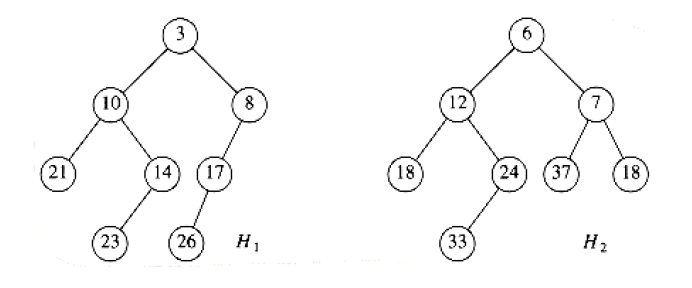
In the below example, we want to merge two skew heaps \(H_1\) and \(H_2\):

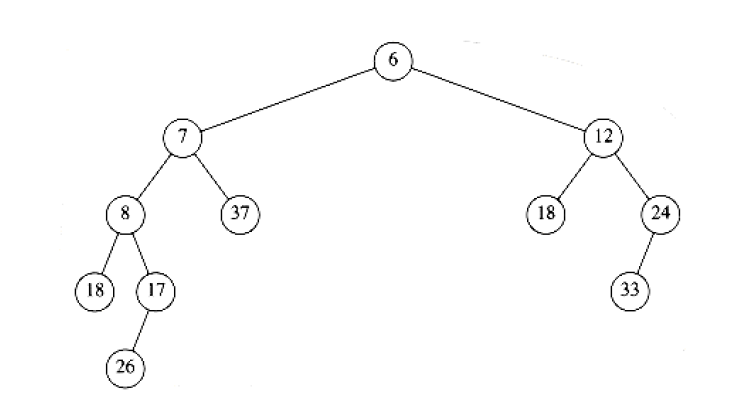
Then, we get the following result of merging \(H_2\) with \(H_1\)'s right subheap:

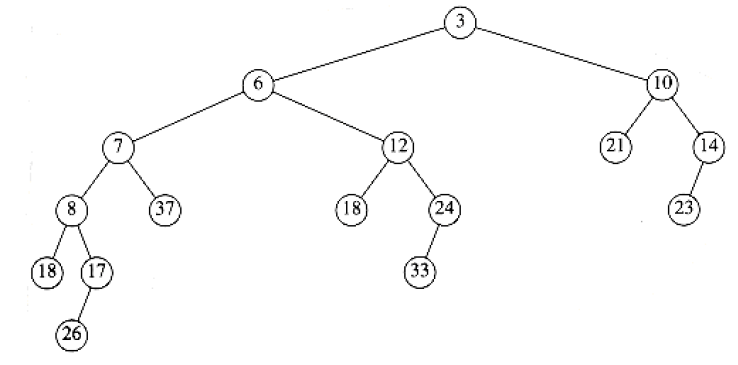
and this is the final merge result:

Runtime analysis

• merge, deleteMin, and insert are all running in \(O(\log N)\) amortized time.

Links to resources

Here are some of the resources I found helpful while preparing this article:

• MAW Chapter 6
• CMU lecture slides