This is the summary of binomial queue part in MAW Chapter 6.

Motivation

We want to have a data structure that support merging, insertion, and deleteMin in \(O(\log N)\) time per operation, and at the same time, like binary heap, we want to have insertion takes constant time on average. The latter part is not possible with skew heap or leftist heap.

The data structure we have is called binomial queue.

Concept

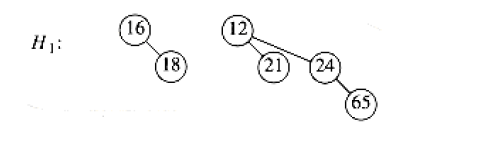
Binomial queues is a collection of heap-ordered trees. Each of the heap-ordered trees is called a binomial tree with the following constraints:

• There is at most one binomial tree of every height.
• A binomial tree of height 0 is a one-node tree; a binomial tree, \(B_k\), of height \(k\) is formed by attaching a binomial tree, \(B_{k-1}\), to the root of another binomial tree, \(B_{k-1}\).

The picture below shows a binomial queue consisting of six elements with two binomial trees \(B_1\) and \(B_2\):

Properties

• A binomial tree \(B_k\), consists of a root with children \(B_0, B_1, \dots, B_{k-1}\).
• Binomial trees of height \(k\) have exactly \(2^k\) nodes
• The number of nodes at depth \(d\) is the binomial coefficient \({k \choose d}\).
• A priority queue of any size can be represented by a collection of binomial trees. For instances, a priority queue of size 13 could be represented by \(B_3, B_2, B_0\) ( \(13 = 2^3 + 2^2 + 2^0\) ). Thus, we can write this representation as \(1101\), which not only represents \(13\) in binary but also represents the fact that \(B_3, B_2, B_0\) are present and \(B_1\) is not.

Operations

Merge

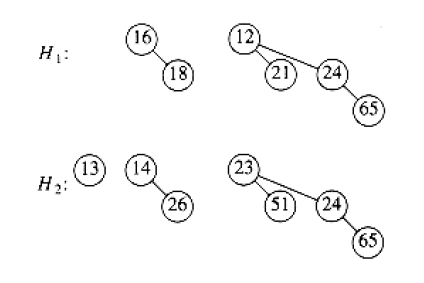
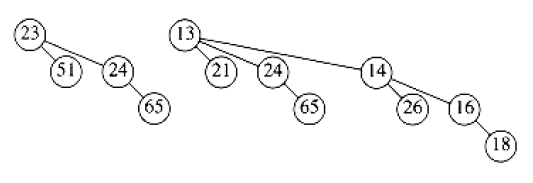
The merge is performed by essentially adding the two queues together. Let's illustrate through merging two binomial queues \(H_1\) and \(H_2\) shown below:

If you will, \(H_1\) can be represented as \(0110_{2}\) and \(H_2\) can be represented as \(0111_{2}\). Thus, merge is just adding two binary number together, and we have \(1101_2\). This implies that our final result contains \(B_0, B_2, B_3\). The actual merge step is implied by the binomial tree constraint mentioned above:

A binomial tree of height 0 is a one-node tree; a binomial tree, \(B_k\), of height \(k\) is formed by attaching a binomial tree, \(B_{k-1}\), to the root of another binomial tree, \(B_{k-1}\).

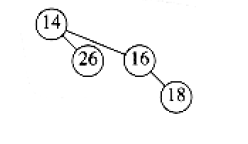
Thus merge of the two \(B_1\) trees in \(H_1\) and \(H_2\) looks like:

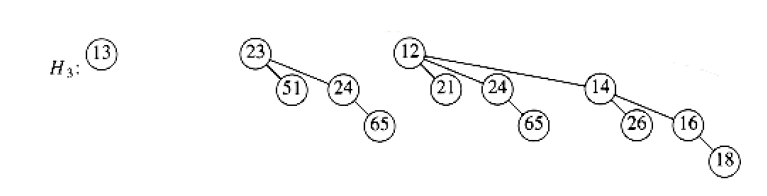
and the final result of merging looks like:

Insertion

Insertion is just a special case of merging, since we merely create a one-node tree and perform a merge.

DeleteMin

1. find the binomial tree with the smallest root. Let this tree be \(B_k\), and let the original priority queue be \(H\).
2. Remove the binomial tree \(B_k\) from the forest of trees in \(H\), forming the new binomial queue \(H'\).
3. Remove the root of \(B_k\), creating binomial trees \(B_0, B_1, \dots, B_{k-1}\), which collectively form priority queue \(H''\).
4. merge \(H'\) and \(H''\).

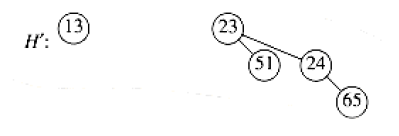
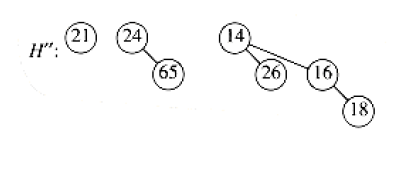
Suppose we perform a DeleteMin on \(H_3\) from above. The minimum root is 12, and we have \(H'\) and \(H''\) below:

and our final result is ¹:

Runtime analysis

Merge

Since merging two binomial trees takes constant time with almost any reasonable implementation, and there are \(O(\log N)\) binomial trees (think of representing the size of priority queue in terms of binary, and we need to do \(O(\log N)\) division), the merge takes \(O(\log N)\) time.

Insertion

The worst-case time of this operation is \(O(\log N)\). However, this actually can be constant on average. Details see MAW p.205.

DeleteMin

We take \(O(\log N)\) time to find the tree containing the minimum element. We take constant time to create the queues \(H'\) and \(H''\). Merging these two queues takes \(O(\log N)\) time and thus, the operation overall takes \(O(\log N)\).

Reference

• MAW Chapter 6