This is the summary of binary heap and its generalization d-heap part in MAW Chapter 6.

Motivation

The motivation for priority queue majorly comes from the fact that not all things are equally weighted. I'll summarize the applications of priority queues in my end-chapter summary post.

Concept

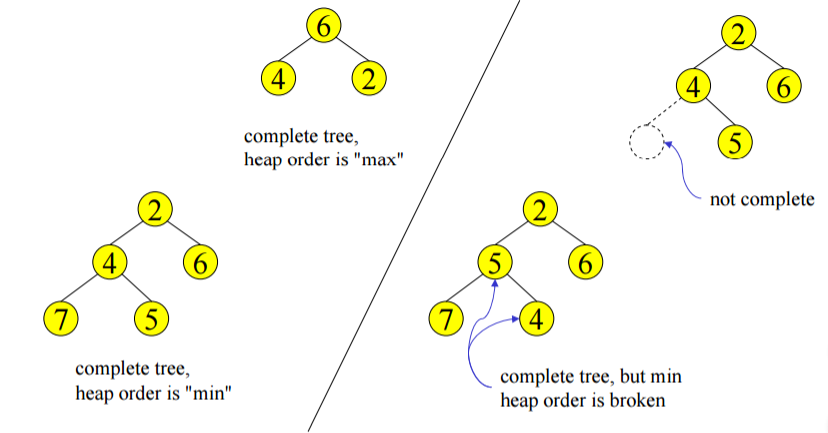
A binary heap is a binary tree (NOT a BST) that is:

• Complete (structure property):

the tree is completely filled except possibly the bottom level, which is filled from left to right.

• satisfies the heap order property:

For every nodex \(X\), the key in the parent of \(X\) is smaller than (or equal to) the key in \(X\), with the exception of the root (which has no parent). In other words, every node is less than or equal to its children.

This property guarantees that the root node is always the smallest node ¹.

Here are some examples:

Properties

• Since complete binary tree of height \(h\) has between \(2^h\) and \(2^{h+1}-1\) nodes, the height of a binary heap is \(O(\log N)\).
• For binary heaps, BuildHeap does at most \(2N-2\) comparisons between elements.

Remarks on implementation

We use array as the actual implementation for the binary heap above. For any element in array position \(i\), the left child is in position \(2i\), the right child is in the cell after the left child \((2i+1)\), and the parent is in position \(\lfloor i/2 \rfloor\). Position 0 is used as a sentinel.

The reason we use the array implementation is that dealing with pointers are quite expensive to do.

Operations

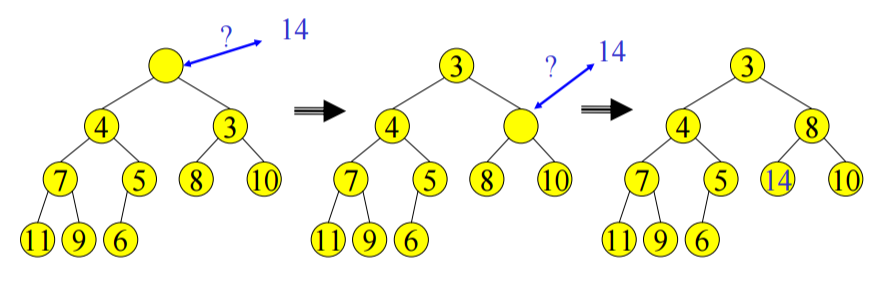
Insert

We add the value as the new node at the end of the array, which is the next avaliable location in the tree. Then, we need to maintain the heap order property by doing a simple insertion sort operation on the path from the new place to the root to find the correct place for it in the tree. This is called percolate up ².

• We start at last node and keep comparing with parent \(A[i/2]\)
• If parent larger, copy parent down and go up one level
• Done if parent \(\le\) item or reached top node \(A[1]\)

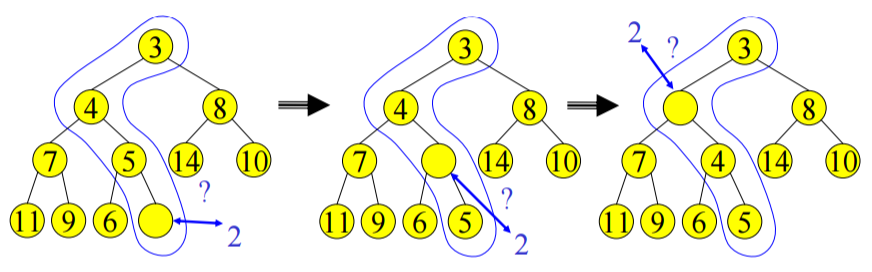
DeleteMin

We delete and return the value at root node in this operation. Same as the insert, we need to maintain the binary heap properties.

By removing the root node's value, we have a "hole" at the root. We use the last node's value in the tree to fill in the hole. By doing this way, we maintain the structure property. Now, we need to maintain the heap order property. Similar to insertion, we can do a simple insertion sort-like operation to find the correct place for it in the tree. This is called percolate down.

• Keep comparing with children \(A[2i]\) and \(A[2i+1]\)
• Copy smaller child up and go down one level
• Done if both children are \(\ge\) item or reached a leaf node

Other heap operations

The following operations (with \(P\) argument) require the position of every element in the heap known by some other method in order to make them cheap to perform.

DecreaseKey(P, \(\delta\), H)

decrease the key value of node at position \(P\) by a positive amount \(\delta\). We can first subtract \(\delta\) from current value at \(P\). Then we percolate up to fix. This requires \(O(\log N)\) time.

IncreaseKey(P, \(\delta\), H)

increase the key value of node at position \(P\) by a positive amount \(\delta\). We can add \(\delta\) to current value at \(P\) then percolate down to fix. This requires \(O(\log N)\) time.

Delete(P,H)

removes the node at position \(P\) from the heap. We can use DecreaseKey(P, \(\infty\), H) followed by DeleteMin. The running time is \(O(\log N)\).

Buildheap(H)

takes as input \(N\) keys and construct a binary heap from it. This is known as Floyd's algorithm.

• Place the \(N\) keys into the tree in order. This satisfies the structure property.
• Then we do the following to maintain the heap order property.

for( i = N/2; i > 0; i--)
  PercolateDown(i);

This alogrithm runs in \(O(N)\) time. Detailed proof see MAW p.189.

Merge(H1,H2)

We merge two heaps \(H1\) and \(H2\) of size \(O(N)\). \(H1\) and \(H2\) are stored in two arrays. We can do \(O(N)\) insert but this requires \(O(N\log N)\) time. We can do better by copy \(H2\) at the end of \(H1\) and use BuildHeap. This requires \(O(N)\) time ³.

Runtime analysis

• Space: \(O(N)\) (an array of size \(N+1\))

• Insert: \(O(\log N)\)

• DeleteMin: \(O(\log N)\)

d-heaps

d-heaps is the generalization of binary heap: we have \(d\) children instead of 2. Similar to B-tree, this structure will makes the heaps shallower and is useful for heaps too big for memory.

Everything is same to the binary heap except that it takes \(d-1\) comparisons to find the minimum of \(d\) children (in binary heap, we do comparison once). Then, for DeleteMin, for example, takes \(O(d\log_d N)\). Other operations runtime adjusts similarly.

In terms of array implementation, for entry located in position \(i\), the parent is at \(\lfloor{\frac{i + (d-2)}{d}}\rfloor\) and the children are at \(id-(d-2), \dots, id+1\).

Links to resources

Here are some of the resources I found helpful while preparing this article:

• MAW Chapter 6
• Lecture slides 4, 8, and 11 from U.Washington