Leftist heap
This is the summary of leftist heaps part in MAW Chapter 6.
Motivation
Merge two priority queues into one can be a very hard operation to do. For binary heap, this can be done at \(O(N)\). However, we want to do better. Leftist heap is a priority queue that supports merge operation in \(O(\log N)\).
Concept
The idea for leftist heap is that we want to make the tree structure imbalance as much as possible to make merge fast. This is achieved by leftist heap property.
-
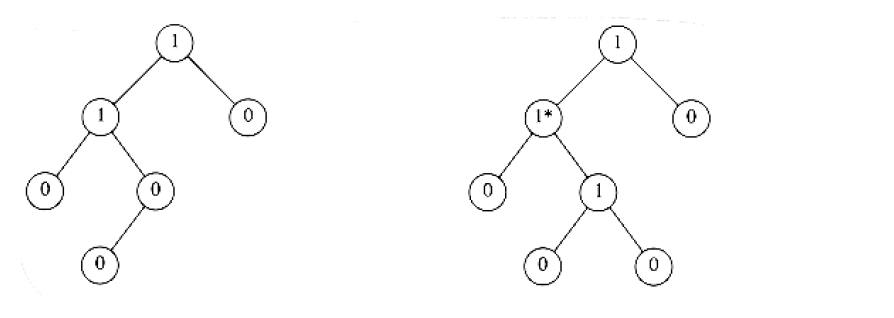
null path length \(Npl(X)\) of any node \(X\) is the length of the shortest path from \(X\) to a node without two children. Thus, the \(Npl\) of a node with zero or one child is 0 and \(Npl(NULL) = -1\). In addition, the \(Npl\) of any node is 1 more than the minimum of the \(Npl\) of its children.
-
leftist heap property is that for every node \(X\) in the heap, the \(Npl\) of the left child is at least as large as that of the right child.
In fact, the leftist heap property is the leftist property applies to heap. In other words, if every node in a tree has the \(Npl\) of the left child is at least as large as that of the right child, then we call this tree a leftist tree. A leftist heap is simply a leftist tree with keys in heap order.
The number in the each node below is the \(Npl\) of that node. By the leftist property, only the left tree is leftist.
Properties
- If rightmost path of leftist tree has \(r\) nodes, then the whole tree has at least \(2^r-1\) nodes.
The above property leads to: \(n \ge 2^r-1\), so \(r\) is \(O(\log N)\). Since our fundamental operation
mergewill perform all the work on the right path, then we can have a \(O(\log N)\)mergeoperation.
- A perfectly balanced tree forms if keys 1 to \(2^k-1\) are inserted in order into an initially empty leftist heap.
Operations
merge(H1, H2)
As with splay in splay trees, merge is
the fundamental operation that is used to implement other operations in leftist
heap(i.e., insert, deleteMin).
The key point for the merge operation are:
-
recursively merge the heap with the larger root with the right subheap of the heap with the smaller root.
-
We update \(Npl\) of the merged root and swap left and right subtrees just below root, if needed, to keep leftist property of merged result.
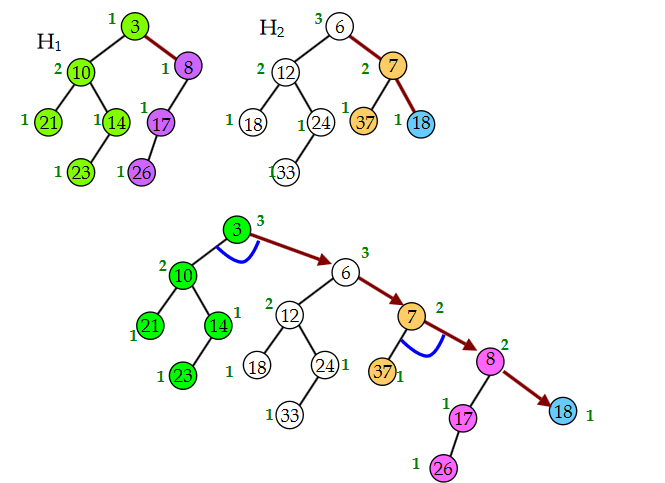
The following picture shows a good example of merge steps. Note that the \(Npl\) of the node in
picture is 1 larger than our's definition. The blue curve represents the final
swap step.
Another example can be seen from MAW 6.16 in my chapter 6 writing question post.
The actual implementation in C is below, which is copied from maw p.198:
PriorityQueue
Merge(PriorityQueue H1, PriorityQueue H2)
{
if (H1 == NULL) return H2;
if (H2 == NULL) return H1;
if (H1->Element < H2->Element) return Merge1(H1, H2);
if (H1->Element > H2->Element) return Merge1(H2, H1);
}
static PriorityQueue
Merge1(PriorityQueue H1, PriorityQueue H2)
{
if (H1->Left == NULL) H1->Left = H2; // Single node; H1->Right is already NULL
else
{
H1->Right = Merge(H1->Right, H2);
if(H1->Left->Npl < H1->Right->Npl) swapChildren(H1);
H1->Npl = H1->Right->Npl + 1;
}
return H1;
}
insert
We can carry out insertion by making the item to be inserted a one-node heap and perform a merge.
Reference section offers a link to visualize the whole insertion process. The actual implementation is on maw p.199 and copied below:
PriorityQueue
Insert1(ElementType X, PriorityQueue H)
{
PriorityQueue SingleNode;
SingleNode = malloc(sizeof(struct TreeNode));
assert(SingleNode);
SingleNode->Element = X; SingleNode->Npl = 0;
SingleNode->Left = SingleNode->Right = NULL;
H = merge(SingleNode, H);
return H;
}
deleteMin
deleteMin can be done by remove the root and merge the left and subtree tree into a new leftist heap.
The actual implementation is on maw p.200 and copied below:
PriorityQueue
DeleteMin(PriorityQueue H)
{
PriorityQueue LeftHeap, RightHeap;
if(IsEmpty(H))
{
Error("Priority queue is empty");
return H;
}
LeftHeap = H->Left;
RightHeap = H->Right;
free(H);
return Merge(LeftHeap, RightHeap);
}
BuildHeap
As described in MAW 6.22, we can perform BuildHeap in linear time for leftist
heaps by considering each element as a one-node leftist heap, placing all these
heaps on a queue, and performing the following step: Until only one heap is on
the queue, dequeue two heaps, merge them, and enqueue the result.
This algorithm is \(O(N)\) in the worst time.
Runtime analysis
merge,deleteMin, andinsertare all running in \(O(\log N)\).
Reference
- MAW Chapter 6
- http://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/heaps.pdf
- https://www.cs.usfca.edu/~galles/visualization/LeftistHeap.html (good tool to visualize the operations)
- http://courses.cs.washington.edu/courses/cse326/08sp/lectures/05-leftist-heaps.pdf