MAW Chapter 6: Priority Queues (Heaps) writing questions

Solutions

including: MAW 6.6, 6.7, 6.9, 6.13, 6.14, 6.16, 6.17, 6.27, 6.28,

MAW 6.6

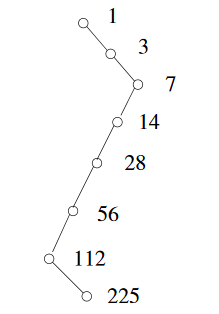
How many nodes are in the large heap in Figure 6.13?

This question is interesting in the sense that the algorithm of counting reflecting the underneath implemenation structure. Since the binary heap is actually implemented in terms of array, we start with $i = 1$ and position at the root. We follow the path toward the last node, doubling $i$ when taking a left child, and doubling $i$ and adding one when taking a right child. Then, we have the following calculation: $2(2(2(2(2(2(2i+1)+1)))))+1 = 225$. The picture below shows the path from the root to the node in the last position:

MAW 6.6

MAW 6.7

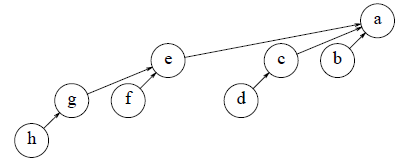
b. show that a heap of eight elements can be constructed in eight comparisons between heap elements.

Thie question is interesting because it offers another method we can use when build a binary heap with even number of elements. That is, we build binomial queue first. since the binary form of $8$ is $1000_2$, this means we will have only one binomial tree $B_3$ inside the binomial queue. Once we construct this binomial tree, we need one last step to tweek the binomial tree to follow binary heap property, namely each node has to have either zero or two children.

For this question, it takes seven comparisons to construct the binomial queue (with a solo binomial tree) and we get the following:

MAW 6.7.b

Then we need to restore the binary heap property because "a" node has three children. This can be done by the eighth compariosn between "b" and "c". If "c" is less than "b", then "b" is made a child of "c". Otherwise, both "c" and "d" are made children of "b".

MAW 6.9

a. Give an algorithm to find all nodes less than some value, X, in a binary heap. Your algorithm should run in $O(K)$, where $K$ is the number of nodes output.

The big idea is that we perform a preorder traversal of the heap. In detail, we start from the root of the heap. If value of the root is smaller than $X$, then we output this value and call procedure recursively once for its left child and once for its right child. If the value of a node is bigger or equal than $X$, then the procedure halts without printing the value. We don't need to check the children by heap definition.

The complexity of this algorithm is $O(N)$ in worst case, where $N$ is the total number of nodes in the heap. This happens when every node in the heap is smaller than $X$, and the procedure has to call each node of the heap.

b. Does your algorithm extend to any of the other heap structures dicussed in this chapter?

Yes. It works for leftist heap, skew heap, and d-heaps.

MAW 6.13

If a d-heap is stored as an array, for an entry located in position $i$, where are the parents and children?

Let's begin with children. Assume that position $i$ corresponds to the $X$th node of level $l$. Therefore

$$ i = \sum_{j=0}^{l-1}d^j+X $$

$\sum_{j=0}^{l-1}d^j$ is a geometric series whose first term equals $1$, whose common ratio is $d$, and that contains $l$ terms in total. Thus, the result is $\frac{d^l-1}{d-1}$ and thus, we have

$$ i = \frac{d^l-1}{d-1} + X $$

We now calculate the position of $i$'s second last child in terms of $d$, $l$, and $X$. This equals $i$, plus the number of nodes after $i$ on level $l$, plus $d$ times the number of nodes before $i$ on level $l$, plus $d-1$.

$$ \begin{eqnarray*} &=& \frac{d^l-1}{d-1} + X + d^l - X + (X-1)d + d - 1 \\ &=& \frac{d^l-1}{d-1} + d^l-1 + dX \\ &=& \frac{d(d^l-1)}{d-1} + dX \\ &=& d(\frac{d^l-1}{d-1} + X) \\ &=& di \end{eqnarray*} $$

Therefore the second last child of $i$ is in position $id$. It follows that the children of $i$ are in positions $id-(d-2), \dots, id+1$.

A node is a child of $i$ if and only if it is in one of the positions $id-(d-2), \dots, id+1$. So what you want here is a function that will map each of these to $i$, but will not map any other value to $i$. Let $j$ be any of these values. Clearly,

$$ \lfloor{\frac{j + (d-2)}{d}}\rfloor = i $$

But if $j$ is greater than $id+1$ or less than $id - (d-2)$ then

$$ \lfloor{\frac{j + (d-2)}{d}}\rfloor \ne i $$

Thus we have our function which can now be used to work out the position of the parent of $i$.

$$ \lfloor{\frac{i + (d-2)}{d}}\rfloor $$

MAW 6.14

Suppose we need to perform $M$ PercolateUp and $N$ DeleteMiin on a d-heap that initially has $N$ elements.

a. What is the total running time of all operations in terms of $M$, $N$, and $d$?

A percolateUp operation on a d-heap with $N$ elements takes $O(\log_d N)$ steps. The key is that each time we bubble the hole up, we only do comparison once: compare the insertion value with the parent of the hole (Figure 6.6, 6.7 helps understanding).

A deleteMin operation on a d-heap with $N$ elements takes $O(d \log_d N)$ steps. Here, we need to feel the empty hole with the minimum value of its children. This can take $d$ comparison to find the minimum (see p.184).

Thus in total this will take $O(M\log_d N + Nd\log_d N)$ steps.

b. If $d = 2$, what is the running time of all heap operations?

Substitute 2 into the formula calculated in part a) gives $O((M+N)\log_2 N)$.

c. If $d = \theta (N)$, what is the total running time?

If $d = \theta (N)$ then $d = cN$, where $c$ is a constant value independent of $N$. Substituting $cN$ into the formula calculated in part a) gives:

$$ M\log_{cN} N + NcN \log_{cN}N = O(M + N^2) $$

d. What choice of $d$ minimizes the total running time?

$d = max(2, M/N)$ (See the related discussion at the end of Section 11.4)

MAW 6.16

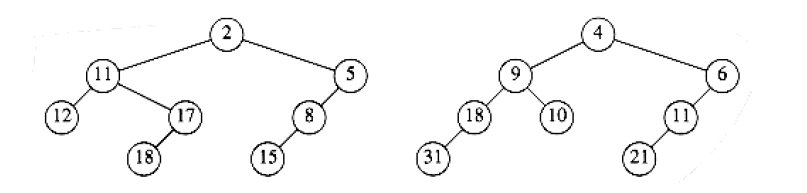
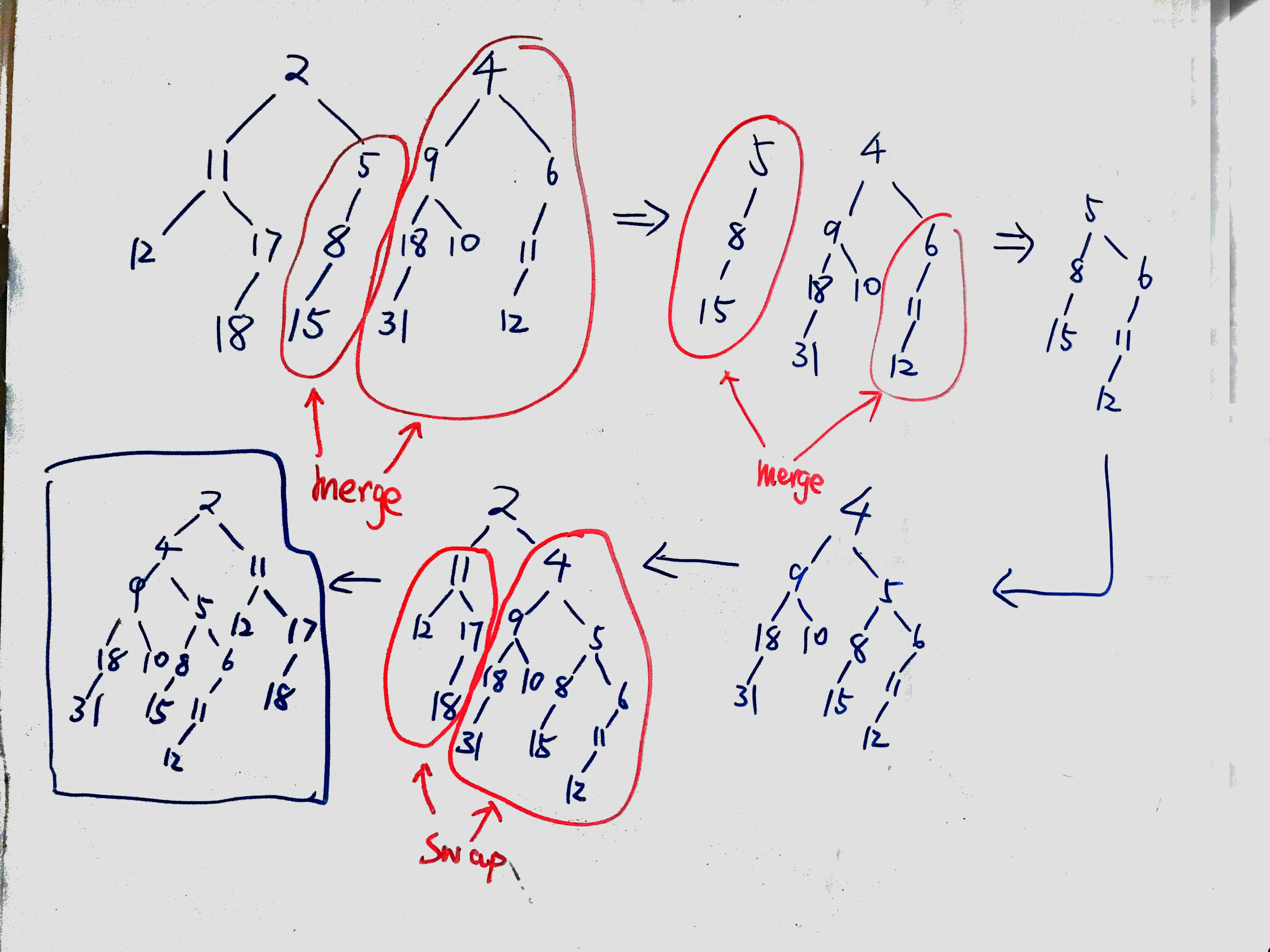
Merge the two leftist heaps in Figure 6.58

MAW 6.16

The book doesn't do a well job on displaying the detailed steps in merging the leftist heap. So, I decide to use this problem as an illustration. By algorithm description on p. 194 and the actual algorithm implementation on p.189., there are two key points in the algorithm:

recursively merge the heap with the larger root with the right subheap of the heap with the smaller root.
We do the swap at the root.

The following shows the steps to get the final answer for this problem:

MAW 6.16 solution

MAW 6.17

Show the result of inserting keys 1 to 15 in order into an initially empty leftist heap.

Use this wonderful site to see the whole process of insertion.

MAW 6.27

Prove that a binomial tree $B_k$ has binomial trees $B_0, B_1, \dots, B_{k-1}$ as children of the root.

I'll try to use two ways to prove this. Both ways are by induction but one of them is more mathematical formula involved.

Method 1

Clearly the claim is true for $k = 1$. Suppose it is true for all values $i = 1, 2, \dots, k-1$. Since for $B_k$, we have $2^k$ nodes. Then, by the induction hypothesis, we have $2^{k-1} = 1 + 2^0 + \dots + 2^{k-2}$. Now, multiplying both sides of the equation by 2, we have $2^k = 2 + 2 + \dots + 2^{k-1}$, which is the same as $2^k = 1 + 2^0 + \dots + 2^{k-1}$. This completes the proof.

Method 2

Again the claim is true for $k = 1$. Suppose it is true for all values $i = 1, 2, \dots, k-1$. A $B_k$ tree is fromed by attaching a $B_{k-1}$ tree to the root of a $B_{k-1}$ tree. Thus, by induction, it contains a $B_0$ through $B_{k-2}$ tree, as well as the newly attached $B_{k-1}$ tree, proving the claim.

MAW 6.28

Prove that a binomial tree of height $k$ has ${k \choose d}$ nodes at depth $d$.

Proof is by induction. Clearly the claim is true for $k=1$. Assume true for all values $i=1,2,\dots,k$. A $B_{k+1}$ tree is formed by attaching a $B_k$ tree to the original $B_k$ tree. The original tree has ${k \choose d}$ nodes at depth $d$ by induction hypothesis. The attached tree had $\binom{k}{d-1}$ nodes at depth $d-1$, which are now at depth $d$. Adding these two terms we have

$$ \binom{k+1}{d} = \binom{k}{d} + \binom{k}{d-1} $$