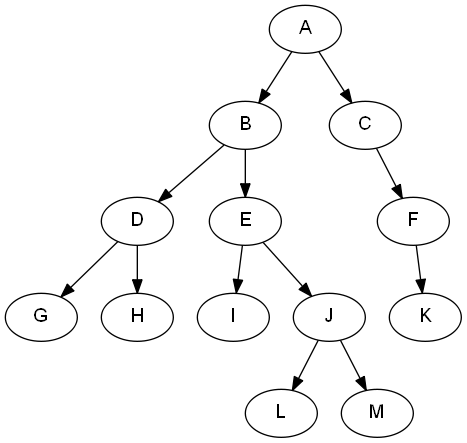
Tree Terminology
Terminology
Like "list" in Chapter 3, "Trees" is another type of abstraction.
tree, root, edge
We can define a tree recursively. A tree is a collection of nodes. The collection can be empty; otherwise, a tree consists of a distinguish node r, called the root, and zero or more nonempty (sub)tress \(T_1\), \(T_2\), ..., \(T_k\), each of whose roots are connected by a directed edge from r.
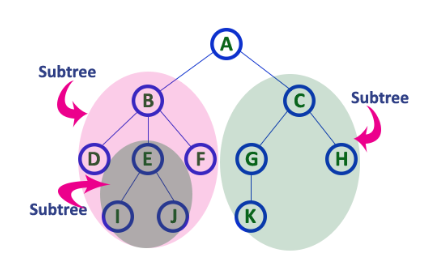
child, parent
The root of each subtree is said to be a child of r, and r is the parent of each subtree root.
leaves
Nodes with no children are known as leaves.
siblings
Nodes with the same parent are siblings.
path
A path from node \(n_1\) to \(n_k\) is defined as a sequence of nodes \(n_1\), \(n_2\), ..., \(n_k\) such that \(n_i\) is the parent of \(n_{i+1}\) for \(1<= i < k\).
length
The length of this path is the number of edges on the path, namely \(k-1\).
Note
- There is a path of length zero from every node to itself.
- Notice that in a tree there is exactly one path from the root to each node.
depth
For any node \(n_i\), the depth of \(n_i\), is the length of the unique path from the root to \(n_i\).
internal path length
The sum of the depths of all nodes in a tree is known as the internal path length.
height
The height of \(n_i\) is the length of the longest path from \(n_i\) to a leaf. (i.e., the height of a node is the number of edges from the node to the deepest leaf)
ancestor, descendant
If there is a path from \(n_1\) to \(n_2\), then \(n_1\) is an ancestor of \(n_2\) and \(n_2\) is a descendant of \(n_1\). If \(n_1 \neq n_2\), then \(n_1\) is a proper ancestor of \(n_2\) and \(n_2\) is a proper descendant of \(n_1\).
internal node
An internal node is a node with at least one child. In other words, internal nodes are nodes other than leaves.
degree
The total number of children of a node is called as degree of that node. The highest degree of a node among all the nodes in a tree is called as degree of tree.
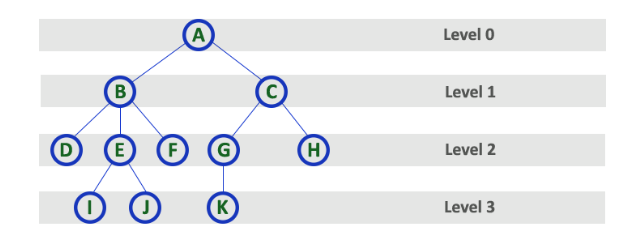
level
The root node is said to be at level 0 and the children of root node are at level 1 and the children of the nodes which are at level 1 will be at level 2 and so on ... In other words, in a tree each step from top to bottom is called as a level and the level count starts with '0' and incremented by one at each level (step).
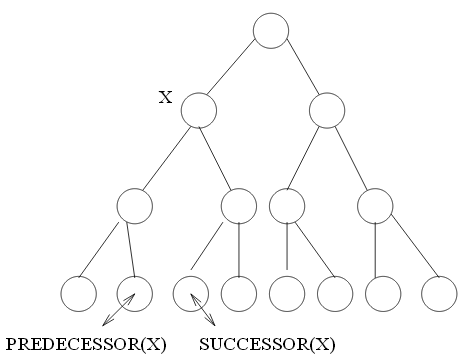
predecessor / successor
If \(X\) has two children, its predecessor is the maximum value in its left subtree and its successor the minimum value in its right subtree. It makes sense if we do in-order traversal of the tree.
Inorder traversal
Given a tree shown below, the inorder traversal (left, root, right) gives: 4, 2, 5, 1, 3
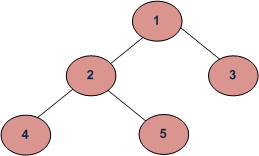
Preorder traversal
Given the same tree above, the preorder traversal (root, left, right) gives: 1, 2, 4, 5, 3
Postorder traversal
Given the same tree above, the postorder traversal (left, right, root) gives: 4, 5, 2, 3, 1
Some properties
- A tree is a collection of N nodes, one of which is the root, and N-1 edges. (since each edge connects some node to its parent, and every node except the root has one parent.)
- The root is at depth 0.
- All leaves are at height 0.
- The height of a tree is equal to the height of the root.
- The depth of a tree is equal to the depth of the deepest leaf; this is always equal to the height of the tree.