Reflection

One important philosophy in this chapter is the separation between the interface exposed to the user and the implementation details behind the scene. The interface exposed to the user is the Abstract Data Types (ADTs). In this chapter, the interface in this chapter is "List". However, there are multiple implementations can meet the requirement of the interface, which are "Array" and "Linked Lists". We can further categorize "List" interface into different subcategories "Stack", "Queue", "Deque". In other words, even we talk about "Stack" ADT, "Queue" ADT, and "Deque" ADT, they are all essentially the "List" but with some restrictions in terms of list operations. Here is a picture that helps us to understand this concept better:

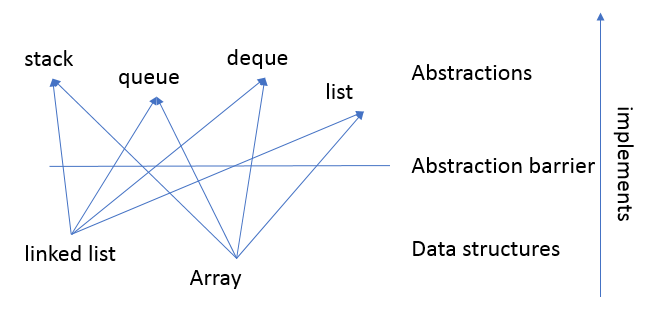
In terms of actual implementation, we can get a sense of what's the basic structure that a data structure should have. Take a linked list implementation of a queue as an example. The key characteristics of a queue is that it should have a \(O(1)\) operation on both enqueue and dequeue. This leads us to the pointer to pointing both the front and rear of the list. Thus, our queue "queue.h" and "queue.c" look like respectively:

struct QueueRecord;
struct QueueCDT;
typedef struct QueueRecord* PtrToNode;
typedef struct QueueCDT* QueueADT;

struct QueueRecord
{
  ET Element;
  PtrToNode Next;
};

struct QueueCDT
{
  PtrToNode Front;
  PtrToNode Rear;
};

Here, our queue pointed by QueueADT is defined by two pointers: Front and Rear. Then, Those two pointers are pointing to our actual QueueRecord, which how we form our linked list implementation. So, when we implement a data structure, we can take a top-down view by first thinking about what characterizes our data structure. That's the very important first step we take. Then, we can think follow the flow naturally by defining what are the required elements to implement those characteristics.

Chapter Structure

Linked List

• Singly Linked List
• Doubly Linked List
• Circular Linked List
• Applications:
  • Polynomial ADT
  • Raxi Sort

Stacks

• Linked List implementation
• Array implementation
• Applications:
  • Balancing Symbols
  • Postfix Expression (Postfix expression evaluation; Infix to Postfix Conversion)
  • Function Call Stack

Queue

• Array implementation
• Linked List implementation

Notable Questions

• 3.4, 3.5

  implement set operations using "List" interface. Especialy the union one provides insights on how we can implement addition of polynomials (3.6) and integer addition (3.9)

• 3.6, 3.7, 3.8, 3.9

  a set of problems relating to Polynomial ADT

• 3.10, 3.24

  problems to practice recurrence relation. Josephus problem is particular interesting because it's a good combination of mathematics, algorithm (dynamic programming) and data structures.

• 3.12, 3.21, 3.23

  commonly-seen interview questions

• 3.13

  require us to actually implement a radix sort in a real problem.

• 3.18

  balancing symbols using Stack. A really cool problem that the end-product is a tool that you can use in your daily work.

• 3.19, 3.20

  Postfix, Infix related problems. Learn about "shunting yard" algorithm and how left associate operators (i.e +, -) is different from right associate operators (i.e ^) in terms of implementation.

• 3.25, 3.26

  Implement Queue and its variation, Deque, using different data structures. In particular, circular array implementation.

Left Out

Some material I left out when I work through this chapter:

• function calls as an example of stack (this part is going to be covered from computer system point of view in the coming posts).
• cursor implementation of linked list (this part is not on the top priority for now).
• 3.7.c, 3.14, 3.16, 3.18.a, 3.22.b